Points Where The Tangent Line Is Horizontal

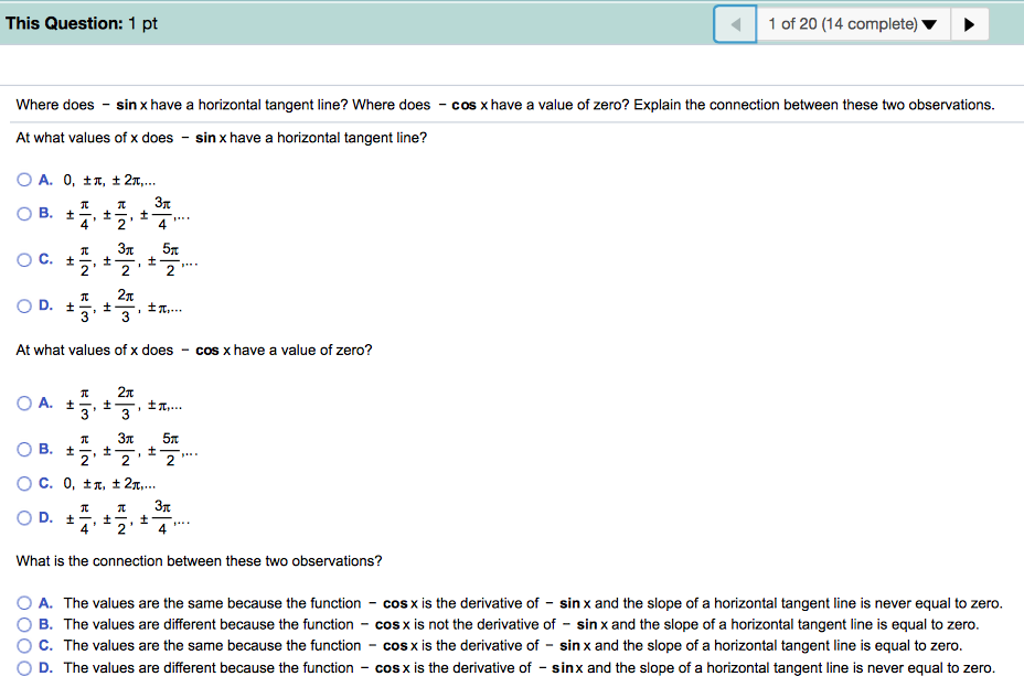
A horizontal tangent line is a mathematical feature on a graph, located where a function's derivative is zero. This is because, by definition, the derivative gives the slope of the tangent line. Therefore, when the derivative is zero, the tangent line is horizontal.

To find horizontal tangent lines, use the derivative of the function to locate the zeros and plug them back into the original equation. Horizontal tangent lines are important in calculus because they indicate local maximum or minimum points in the original function. In terms of the W function, which was developed specifically to solve equations of this type. While there does exist a general algebraic method for computing derivatives, there is no general algebraic method for solving equations.

Even for polynomials, it is known that there can be no generally useful algebraic method of finding roots (i.e., there can be no analog of the quadratic formula) for degree five or above. This is why it is often necessary to resort to numerical approximation methods to solve algebraic equations. Thus, equations of the tangents to graphs of all these functions, as well as many others, can be found by the methods of calculus. The formulas above fail when the point is a singular point. In this case there may be two or more branches of the curve that pass through the point, each branch having its own tangent line. Since any point can be made the origin by a change of variables this gives a method for finding the tangent lines at any singular point.

We'll also look at where to find vertical tangent lines, and where to find horizontal tangent lines, since that's something you'll be asked to do often. Horizontal tangent lines exist where the derivative of the function is equal to 0, and vertical tangent lines exist where the derivative of the function is undefined. There are two things to stay mindful of when looking for vertical and horizontal tangent lines. In the case of horizontal tangents, you will want to make sure that the denominator is not zero at either thexorypoints. In the case of vertical tangents, you will want to make sure that the numerator is not zero at either thexory points. The geometrical idea of the tangent line as the limit of secant lines serves as the motivation for analytical methods that are used to find tangent lines explicitly.

The question of finding the tangent line to a graph, or the tangent line problem, was one of the central questions leading to the development of calculus in the 17th century. Determine the \(x\)-\(y\) coordinates of the points where the following parametric equations will have horizontal or vertical tangents. A horizontal tangent line is parallel to the x-axis and shows where a function has a slope of zero. You can find these lines either by looking at a graph or by setting an equation to zero to find maximums and minimums.

For any constant C, we see that all the tangent line segments along this line have the same slope, no matter what the value of the independent variable, say t. Another way to look at this is to realize that we can generate infinitely many solutions by taking any one solution and translating its graph left or right. Even when we can't solve an equation, an analysis of its slope field can be very instructive.

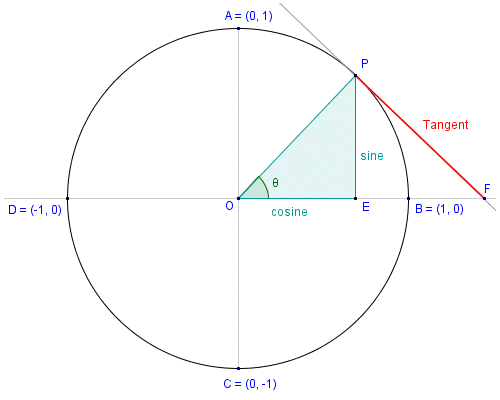
However, such a graphical analysis may miss certain important features of the integral curves, such as vertical asymptotes. The tangent at A is the limit when point B approximates or tends to A. In mathematics, slopes and tangents help determine ratios and rates of change. Learn how to show slopes and tangents as lines on a graph, explore the concept of slope as it pertains to hills, and recognize how slope can be used to describe steepness. The derivative of a function at a point is the slope of the tangent line at this point. The normal line is defined as the line that is perpendicular to the tangent line at the point of tangency.

Because the slopes of perpendicular lines are negative reciprocals of one another, the slope of the normal line to the graph of f is −1/ f′. Knowing the slopes of tangent lines at various points on the graph of a function can help one better understand the graph of the overall function. Newton's method (also called the Newton–Raphson method) is a way to find x-intercepts of functions. In other words, you want to know where the function crosses the x-axis. The method works well when you can't use other methods to find zeros of functions, usually because you just don't have all the information you need to use easier methods.

While Newton's method might look complex, all you're actually doing is finding a tangent line, then another tangent line, and repeat, until you think you're close enough to the actual solution. In mathematics, particularly calculus, a vertical tangent is a tangent line that is vertical. Because a vertical line has infinite slope, a function whose graph has a vertical tangent is not differentiable at the point of tangency. Using implicit differentiation find y', so that you have a formula for slopes of tangent lines to the graph of the original function. The derivative of a function has many applications to problems in calculus. It may be used in curve sketching; solving maximum and minimum problems; solving distance; velocity, and acceleration problems; solving related rate problems; and approximating function values.

To find the equation of a tangent line, sketch the function and the tangent line, then take the first derivative to find the equation for the slope. Enter the x value of the point you're investigating into the function, and write the equation in point-slope form. Check your answer by confirming the equation on your graph. Differentiate the equation of the circle and plug in the values of x,y in the derivative. Use the slope-point form of the line to find the equation, with the slope you obtained earlier and the coordinates of the point. Intuitively, it seems clear that, in a plane, only one line can be tangent to a curve at a point.

However, in three-dimensional space, many lines can be tangent to a given point. If these lines lie in the same plane, they determine the tangent plane at that point. A tangent plane at a regular point contains all of the lines tangent to that point.

A more intuitive way to think of a tangent plane is to assume the surface is smooth at that point . Then, a tangent line to the surface at that point in any direction does not have any abrupt changes in slope because the direction changes smoothly. There are a few other methods worth going over because they relate to the tangent line equation. Knowing these will help you find the extreme points on the graph, the equation of the normal, and both the vertical and horizontal lines.

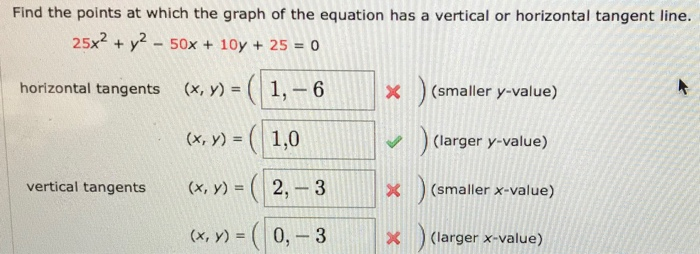
Find the equations of the horizontal tangent lines. The tangent plane to a surface at a given point p is defined in an analogous way to the tangent line in the case of curves. Calculus equations that seek to determine the maximum or minimum value for a given parameter are called optimization problems. Learn about optimization problems through real-world examples/explanations and how to use the six-step method to solve optimization problems in calculus. Separable differential equations are used to rearrange variables so that all terms of one variable are on one side of the equation, thus ''separating'' the variables.

See the steps involved in recognizing and solving these types of differential equations. When studying mathematics functions and methodology of calculation, a good place to start is understanding the significance of one-sided limits and continuity. Learn more about the properties and functions, and study an example of a formula for finding one-sided limits and continuity. Once you have the slope of the tangent line, which will be a function of x, you can find the exact slope at specific points along the graph. The next topic that we need to discuss in this section is that of horizontal and vertical tangents.

We can easily identify where these will occur (or at least the \(t\)'s that will give them) by looking at the derivative formula. Unlike a straight line, a curve's slope constantly changes as you move along the graph. To find the equation for the tangent, you'll need to know how to take the derivative of the original equation. Drag the red point to see how the tangent changes along the curve.

Drag the green point to see how the secant line approaches the tangent as the green dot approaches the red dot . Not also how each of the slopes of the tangent and secant lines change . However, there are examples of situations where the tangent line does cut across the curve. The simplest examples are those involving a point of inflection where the curve changes its sense of concavity, such as the cube map at the origin. More complicated examples involve points where the second derivative of the function is oscillating sign very rapidly very close to the point, such as functions of the form .

If both the derivatives are zero, then we try to see if exists and is finite, and if so, take that as the derivative that we plug into the equation for the tangent line. If it is a single signed infinity, we get a vertical tangent. Congratulations on finding the equation of the tangent line! You can now be confident that you have the methodology to find the equation of a tangent.

It may seem like a complex process, but it's simple enough once you practice it a few times. The key is to understand the key terms and formulas. Having a graph as the visual representation of the slope and tangent line makes the process easier as well. When looking for a vertical tangent line with an undefined slope, take the derivative of the function and set the denominator to zero. Vertical tangent lines occur at the points (-4, -1) and (2, -1).

No, the curve cannot have a horizontal tangent where it crosses the x-axis. Use a straight edge to verify that the tangent line points straight up and down at that point. If the right-hand side of the equation differs from the left-hand side , then there is a vertical tangent line at that point. The fundamental theorem of calculus allows us to calculate indefinite integrals as the anti-derivatives of the original polynomial function. Learn how to calculate indefinite integrals of polynomials through several examples and how to apply a general rule to polynomials with any number of variables. In calculus, differential approximation is a way to approximate the value of a function close to a known value.

It is just another name for tangent line approximation. In other words, you could say "use the tangent line to approximate a function" or you could say "use differentials to approximate a function"; They mean the same thing. The vertical tangent to a curve occurs at a point where the slope is undefined . This can also be explained in terms of calculus when the derivative at a point is undefined. Understanding the nature of slopes of tangent lines to functions can raise red flags when appropriate to alert us to not be so quick to believe what we see on our calculator screens. When working with a function of two variables, the tangent line is replaced by a tangent plane, but the approximation idea is much the same.

Use the tangent plane to approximate a function of two variables at a point. When looking for a horizontal tangent line with a slope equating to zero, take the derivative of the function and set it as zero. To find out where a function has either a horizontal or vertical tangent, we will have to go through a few steps. While you can be brave and forgo using a graph to illustrate the tangent line, it will make your life easier to graph it so you can see it. This is because it makes it easier to follow along and identify if everything is done correctly on the path to finding the equation. You will want to draw the function on graph paper, with the tangent line going through a set point.

In regards to the related pursuit of the equation of the normal, the "normal" line is defined as a line which is perpendicular to the tangent. This line will be passing through the point of tangency. A cusp corresponds to a "corner" or abrupt change in direction of a curve representing a function that is continuous at the point in question. The curve has different tangents immediately to the right and left of a cusp. 2) Plug x value of the indicated point into f ' to find the slope at x. 3) Plug x value into f to find the y coordinate of the tangent point.

4) Combine the slope from step 2 and point from step 3 using the point-slope formula to find the equation for the tangent line. What's basically happening with this equation is each iteration takes you closer and closer to the true solution, as the following image shows. The blue line is the tangent line for x0 and the green line is the tangent line for the second iteration. Eventually, your answers will get closer and closer to the red x-value. The instantaneous rate of change is the slope of the tangent line at a point. A derivative function is a function of the slopes of the original function.

To find the points at which the tangent line is horizontal, we have to find where the slope of the function is 0 because a horizontal line's slope is 0. Now set it equal to 0 and solve for x to find the x values at which the tangent line is horizontal to given function. The below image shows three such secants $\overline$, $\overline$, and $\overline$. Note, the slopes of these secants do a better job of approximating the slope of the tangent line to the curve at $P$ shown in red as the second point $Q_i$ gets closer to $P$.

So in this sense, calling it a tangent line seems reasonable. However, the red line also intersects the curve in two places, which suggests the reverse if we adhere to the old geometric definition of a tangent line. In each case, the slope of the tangent line corresponds to the rate of change in one variable seen for a particular value of the other.

Notice how the slope of the tangent line at the highest point on the curve below is horizontal. Often, finding places where the tangent line has horizontal slope reveals maximum values. The partial derivatives must therefore exist at that point. However, this is not a sufficient condition for smoothness, as was illustrated in Figure 4.29. In that case, the partial derivatives existed at the origin, but the function also had a corner on the graph at the origin. Furthermore, if a function of one variable is differentiable at a point, the graph is "smooth" at that point (i.e., no corners exist) and a tangent line is well-defined at that point.

We learned about the equation of a plane in Equations of Lines and Planes in Space; in this section, we see how it can be applied to the problem at hand. If a tangent has a positive slope the graph is increasing around the point of tangency. If a tangent has a negative slope the graph is decreasing around the point of tangency.

If a tangent is horizontal the graph is often, but not always, at a peak or trough at the point of tangency. We could estimate the slope of L from the graph, but we won't. Instead, we will use the idea that secant lines over tiny intervals approximate the tangent line.

With this method, the first step you will take is locating where the extreme points are on the graph. These are the maximum and minimum points, given that one is higher than any other points, whereas another is lower than any points. Remember that a tangent line will always have a slope of zero at the maximum and minimum points. In the differential equations and dynamic optimization, where the independent variable is the time. These methods led to the development of differential calculus in the 17th century. Further developments included those of John Wallis and Isaac Barrow, leading to the theory of Isaac Newton and Gottfried Leibniz.

Now write the equation in point-slope form then algebraically manipulate it to match one of the slope-intercept forms of the answer choices. The study of curves can be performed directly in polar coordinates without transition to the Cartesian system. Use a derivative and perpendicular slope of a tangent line to calculate the equation of the normal line. When looking at a graph, the concavity of a function is determined by the changes to its derivative. Learn how to define concavity and inflection points with differentiation by going over a review of concavity and four concavity examples. L'Hopital's Rule helps us solve limits that are not within the range of other problem-solving tools.